テクノ雑学

第71回　秘密の鍵は光に乗せて　−量子暗号の仕組み−

コンピュータネットワークでさまざまな情報がやりとりされるようになり、盗聴されない安全な通信が必要とされています。今回のテクの雑学では、「絶対に安全な暗号化手法」として注目されている量子暗号の仕組みをみてみましょう。

現在使われている暗号理論の限界

現在使われている暗号理論の限界

　「コンピュータで文書を暗号化する」というのは、任意のビット列と文書ファイル（これもビット列です）のデータに一定規則の演算を加えることで、元の文書ファイルとは異なるビット列に変換する操作をいいます。変換時に用いるビット列を「鍵」と呼びます。

　現在、通信時の暗号化に広く使われているPGP（Pretty Good Privacy）では、「公開鍵」と「秘密鍵」という2本セットの鍵を使用します。公開鍵とは文字通り世界中に公開されている鍵で、秘密鍵は所持者が他の人に分からないように所持している鍵です。公開鍵を使って暗号化された文字列は、対応する秘密鍵でしか復号できない仕組みになっています。

　Aさんに暗号化された文書を送るには、まず、Aさんが公開している公開鍵を使って平文（暗号化前の文書）を暗号化します。復号（暗号化された文書を平文に戻す）するためにはAさんが持っている秘密鍵が必要です。すなわち、Aさん以外の人は平文を取り出すことはできないというわけです。

　現在使われているPGPでは、鍵の長さが128bitのものが主流です。この長さの鍵では、公開されている公開鍵の情報から対応する秘密鍵の情報を計算で割り出すためには、数千年単位の膨大な時間がかかるとされています。つまり、現実に第三者に暗号化されたファイルを復号されて困ることはない、だから安全だという理屈です。

　ここで重要なのは、「解読に時間がかかるから安全」だということは、すぐに計算できるようなアルゴリズムができたり、コンピュータの計算能力が向上してしまうと、もっと短時間で鍵を発見される可能性があるということです。実際に、現在研究が進められている量子コンピュータが実用化された場合、計算速度は飛躍的に高まり、現在のPGP方式が一気に無力化されてしまう可能性が指摘されています。

　「時間がかかるから安全」ではなく、理論的に絶対に安全を保証された方式はないのでしょうか。実は、「平文と同じ長さの秘密鍵を1回で使い捨てる」Vernam暗号という方式だけが、絶対に安全な方式であることが理論的に証明されています。

■ 秘密鍵をどうやって渡すか？

　とはいえ問題は、「平文と同じ長さの使い捨ての秘密鍵」が、現実に可能なのかということです。「平文と同じ長さで使い捨ての鍵」が必要であるということは、通信を行うたびに鍵を生成し、その鍵を文書の送信者と受信者で共有しなくてはいけません。しかも、「秘密鍵」ですから、絶対に第三者に知られないように鍵の情報を伝えなくてはいけないのです。

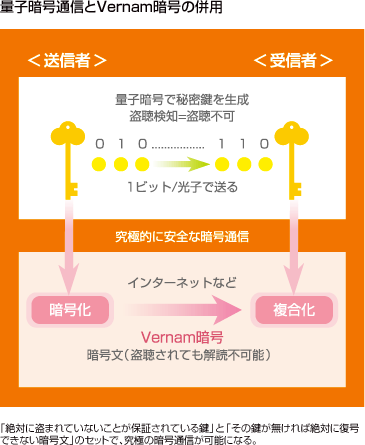
　これを可能にするのが、量子暗号方式です。「秘密鍵」の伝送に量子暗号を使うことで、文書の送信時に生成する鍵の情報を安全に共有し、暗号化された文書は従来使用しているコンピュータネットワークで送信します。鍵の伝送と文書の伝送を別々にするところがこの技術の肝になります。

■ ハイゼンベルグの不確定性原理と量子の観測不可能性

　量子暗号では、具体的には、光子（光の粒子）の状態でビットを表現します。量子暗号が絶対に安全なことは、量子物理学の基本原理である、「粒子の位置と運動量を同時に確定することはできない」というハイゼンベルグの不確定性原理と、「量子は、観測することにより発生する相互作用でその状態を変える」という量子の観測不可能性により保証されるのです。

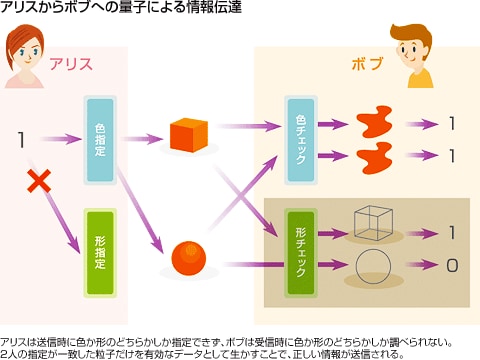
　話を分かりやすくするために、2人の人が、粒子を使って情報を送信する例を考えます。暗号業界の決まりごとでは、送信者がアリス、受信者がボブと決まっているそうですので、それに従いましょう。情報を送る時に使う粒子に「色」と「形」という2つの性質があると考えます。使用する粒子の色が赤い時は1、青い時は0を表すものとし、形が立方体の時は1、球の時は0をあらわしているとします。

　アリスが「1」という情報をボブに送ろうとする時、「色」を指定して粒子を選ぶか、「形」を指定して粒子を選ぶかをランダムに選択できます。「色」と「形」の両方を選択することはできません。これが、ハイゼンベルグの不確定性原理（どちらか一方を確定するともう一方は確定できない）にあたります。

　アリスが「色」を選択した場合、1をあらわす色は「赤」なので、「赤い立方体」か「赤い球」がそれぞれ50％の確率でボブに送られます。どちらが送られたかをアリスは知ることができません。

　受け取ったボブは、送られてきた粒子の「色」を調べるか「形」を調べるかをランダムに選択できます。どちらを選ぶか、確率は50％です。「色」を調べた場合、送られてきているのは形はどうであれ赤いことは間違いないので、100％の確率で「1」という情報が得られます。一方、「形」を調べた場合、不確定性原理により、立方体である確率は50％、球である確率も50％です。つまり、「1」という情報が得られる確率は50％になります。「色」を調べた場合と「形」を調べた場合を総合すると、75％の確率で正しい情報が伝わり、25％の確率で間違った情報が伝わっていることになります。

　ここで、色を調べたのか、形を調べたのかを、ボブはアリスに報告します。アリスは、ボブからの報告で、同じものを調べていれば情報は確実に伝わっているので、その情報を活かします。違うものを調べていた場合は、間違った情報が伝達されている可能性があるので、その情報はお互い破棄してしまいます。

　これを繰り返すことで、任意の個数の粒子を、アリスからボブに送信し、秘密鍵を共有することができます。

■ 盗聴は必ずばれてしまう！

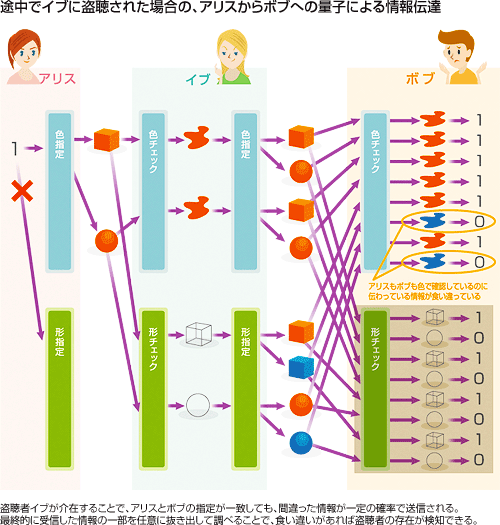
　さてここで、途中に盗聴者イブがいる場合を考えます（暗号業界では盗聴者の名前はイブということに決まっているそうです）。

　途中でイブに盗聴される場合ですが、イブも受信した粒子の色か形、どちらか一方しか調べることができません。つまり、イブは25％の確率で、受け取った粒子の観測結果から、間違った情報を得ることになります。

　一度イブが傍受した粒子は、量子の観測不可能性により、性質が変わってしまっているため、アリスが送ったものとは異なっています。盗聴していることをアリスとボブに気付かれないためには、イブは自分が観測したものと同じ粒子をボブに送信しなおすしかありません。

　しかし、送信時に指定できるのは、「色」か「形」どちらか一方でしかないのです。そして、25％の確率で間違った情報を得ているイブは、一定確率で「青」の粒子を送信してしまう可能性があります。

　イブに盗聴されていないかどうかを確認するためには、アリスとボブは、鍵が完成した後、ランダムなビットをいくつか抜き出して、情報が正しいか間違っているかを確認します（チェックビットの確認）。盗聴されていなければ、情報は100％正しいはずですが、イブに盗聴されていれば、一定確率で間違いが見つかるはずです。この間違いを検出できれば、盗聴されていることが確認できるので、この鍵は使うのを中止して新たな鍵を作り直せばよいのです。

　チェックビットの確認で間違いがないことが確認できれば、その秘密鍵は、絶対に誰にも盗まれていないことが保証されます。従来の暗号のように、「時間がかかりすぎるから事実上解読不可能」なのではなく、物理学的に盗聴されていないことが保証されているのです。

　鍵の共有が完了したら、アリスは、完成した秘密鍵で、文書を暗号化して、光ケーブルなどの通常の通信で送信します。元の平文の長さと同じ長さの秘密鍵で暗号化された文書は、元の秘密鍵を知らなければ復号できないことは数学的に証明されているので、途中で傍受されても第三者に復号されることはありません。暗号化された文書を復号できるのは、秘密鍵を共有しているボブだけです。こうして、理論的に絶対に安全な暗号通信が可能になります。

　実際の量子暗号通信に使われるのは光子で、上の説明の「色」や「形」にあたるものとしては偏光（光の波の向き）、位相、スピンなどさまざまな手法があります。

　1個の光子に情報を載せて一定間隔で送信する必要がありますが、光子1個ということはとても弱い光なので、安定して遠距離に届ける技術が課題になります。2007年6月に、NTT物性科学基礎研究所などのチームが、世界最長の送信距離200kmを達成し、「絶対に安全な暗号」の実用化に向けて大きく前進しました。今後の動向に注目していきたい技術です。

著者プロフィール：板垣朝子（イタガキアサコ）
1966年大阪府出身。京都大学理学部卒業。独立系SIベンダーに6年間勤務の後、フリーランス。インターネットを中心としたIT系を専門分野として、執筆・Webプロデュース・コンサルティングなどを手がける
著書／共著書
「WindowsとMacintoshを一緒に使う本」　「HTMLレイアウトスタイル辞典」（ともに秀和システム）
「誰でも成功するインターネット導入法—今から始める企業のためのITソリューション20事例」（リックテレコム）など