With ferrite by TDK

GRAIN34 ファラデーの困った法則

ファラデーの困った法則

ファラデーの困った法則

これまでに、詳しく見てきたとおり、初透磁率μiの値を極めるためには、2価の鉄イオンが不可欠となる。したがって、経時変化の元凶として2価鉄の存在が疑われたときには、多くの研究者が絶望的な心境に陥った。なにしろ、μiを高めるほど、その減退ぶりは加速し、その事態を避けるためには初めからμiを低く抑えなければならないというのだから、これは絵に描いたような二律背反である。だが、μiの経時変化は、結晶の森にさまよい出た空格子が磁壁に取り込まれていく緩慢なプロセスで生じたマクロ的な意味での誘導磁気異方性による現象であることが明らかとなり、2価鉄に向けられた容疑は晴れたのであった。

空格子による金属イオンの拡散機構を示す簡単なモデルである。金属イオンに見立てた象牙色の駒が欠落している"空格子点"がひとつだけ下方に存在する。そこで、とりあえず右斜め上方の駒をこの空きスペースに降ろせば、この"空格子点"はひと駒分だけ右上方に移動したことになる。いうまでもなく、盤が駒で埋め尽くされていたのではこうした移動は不可能であるが、たったひとつの駒が外されれば、その空白スペースはやすやすと盤上を横切って、いくつめかの手で左上の隅まで到達することができる。温度が高くなるにつれ、そのスピードが一段とアップする事情についても、熱エネルギーを供与されたこれらの駒(金属イオン)が、前後左右に揺れ動く光景を思い描くことで納得できる。つまり、低温においては真面目に水平と直角の移動ルールを守っていた駒が、熱に浮かれた勢いで斜めに滑り込む"ズル"をするようになれば、空格子点もジグザクに移動することなく、一気に盤上を斜めに横切ることができるわけである。

だが、μi衰弱犯の容疑は晴れたものの、自分の電子1個を3価鉄に向けて放出する2価鉄の性癖だけは、いかんともし難く、2価鉄を取り込めば取り込むほど、経時変化とはまったく別の意味で、μiにとってきわめて危うい状況がもたらされることになる。

何がどのように危ういのかといえば、交流磁界の関与により、下のモデルに示すような連鎖的な電子移動、すなわち2価鉄と3価鉄が連続的に入れ替わる電子のホッピング現象が誘起されて、局所で完結していた電子交換に歯止めが効かなくなってしまうのである。

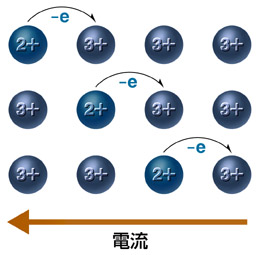
-eの電荷を持つ電子が連続的にホッピングすれば、当然そこには電流が流れることになる。その流れが磁化方位を軸にして渦巻状に発生するので、交流磁界の関与で引き起こされるこのような電気伝導を"渦電流"と呼んでいるが、磁化方位と渦電流の流れる向きの関係は、ファラデーの電磁誘導の法則にしたがうので、下のモデルに示すとおり、この電流は外部磁界と相殺関係となる反磁界Hd(半透明の緑色の矢印)を発生させる向きに流れることになる。

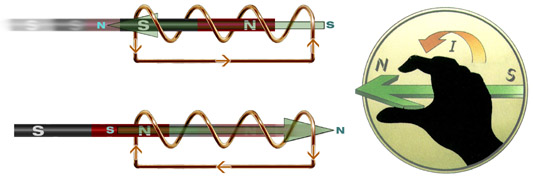
上は磁石がコイルに近づくところを示し、下は反対に磁石がコイルから遠ざかるところを示している。ファラデーにより見出された電磁誘導の法則によれば、閉じられた導体(このモデル図においては閉じたコイル)を貫く磁束の密度が変化するときには、その磁束密度の変化を打ち消す磁束(反磁界Hd)を発生する方向に電流が流れることになる。つまり、磁石のN極をコイルに近づけたときには、コイルの磁石側の端に磁石に反発するようにN極が発生し(上)、反対に磁石のN極を遠ざけると、電流は逆向きに流れ、遠のく磁石を引き戻すようにS極が発生する(下)。

つまり、こうした危険を省みずに2価鉄をふんだんに生成してしまうと、交流磁界(磁界の強さが変わらぬ直流磁界では電磁誘導現象は誘起されない)に誘起された電子のホッピング伝導が活性化し、それに伴い反磁界Hdのパワーも増大することになり、その結果として、交流磁界の実効的なエネルギーは大幅にダウンしてしまうことになる。

その辺りの事情を示したのが、下のグレインモデルである。2価鉄の導入により、電流が流れやすくなるということは、すなわち、フェライトの比抵抗値が低下することを意味している。2価鉄を含まないフェライトの比抵抗値が105Ωmであるのに対し、2価鉄を最も多く含むマグネタイトの比抵抗値は、わずか10-4Ωmであり、2価鉄の"困った性癖"は、こういう側面にも色濃い影を落としている。

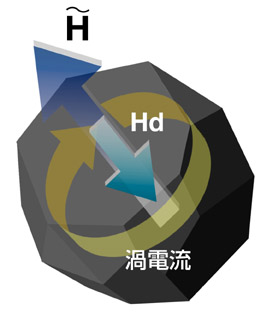
磁界の強さと向きが時間とともに変化する交流磁界を加えることは、磁石を周期的に近づけたり遠ざけたりするのと似た作用を個々のグレインに与えることになる。磁界強度が増すにつれ、グレインの中心部には黄色の矢印で示した渦電流が誘起され、その結果生じる反磁界Hd(グリーンの矢印)のために、交流磁界の実効的な強さはHd分だけ減少してしまうことになる。

反磁界、比抵抗値、いずれの観点から眺めても、結果として交流磁界の"効き具合"が鈍るのだから、過剰な2価鉄の存在は、やはり、まぎれもない損失要因ということになるが、そのあたりの様相をまとめると下の式になる。

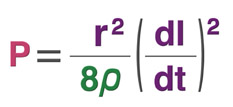
これは、反磁界Hdにより、磁性材料の単位体積あたり、どのくらいの電力損失(p)がもたらされるかを求める式である。磁界方位に対象軸を持つ円柱状の磁性材料を想定して導いた式なので、左の項の分子にあるrは円柱の半径を表わし、同項の分母にある8ρのρは磁性材料の比抵抗値、また、括弧でくくられた右項dI/dtは、時間変化dtあたりの磁化変化dI、すなわち磁化Iの変化速度を示している。つまり、渦電流による交流磁界の電力損失は、磁化Iの変化速度dI/dt(この場合は交流磁界の周波数と同義である)の2乗に比例して増加し、比抵抗値ρに反比例しており、比抵抗値が小さな材料を周波数の高い交流磁界で駆動するときに、損失が最も大きくなることを示している。また、この式によれば、損失は円柱の半径rの2乗にも比例して増大するので、損失を低減するには、磁性材料を細い棒状にしなればならないわけだが、以上の関係を"極小磁性材料"である1個のグレインモデルに置き換えてみると(グレインを磁界方位に対象軸を持つ円柱と見なすわけだが)、グレインの直径をあまり大きく育ててはならない、ということになり、これもまた、2価鉄のジレンマと同じく、ハイμ制御の定石と真向から対立する要求である。

一難去ってまた一難、というわけであるが、じつは、このような電子のホッピング現象は、2価と3価の鉄イオン間ばかりではなく、Mn2+・Fe3+→Mn3+・Fe2+など、価数の変化しやすい陽イオン間でも頻繁に起きる。さて、この難題、いかに料理したものか。

TDKは磁性技術で世界をリードする総合電子部品メーカーです

TDKについて