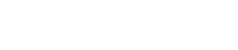With ferrite by TDK

GRAIN23 磁壁を動かすふたつの因子

磁壁を動かすふたつの因子

磁壁を動かすふたつの因子

マクロ的な意味での磁気モーメント(前節で述べた自転する永久磁石モデル)の時間的変化、dM(磁気モーメントの変化)/dt(時間変化)を求める古典力学による運動方程式をトルク方程式と呼ぶが、それは、量子力学的な解釈にもとづき導かれたハイゼンベルグの運動方程式とまったく同じ形になる。このことは、マクロ的な意味での磁気モーメントの運動が、電子固有のスピン磁気モーメントの運動をよく代弁してくれることを示しており、複雑なスピン磁気モーメントの動きをイメージするのに都合が良い。

そこで、いきなりマクロなモデルが、このコマである。地面に垂直に着地したコマは、そのまま回転を続けるが、へたなコマ回しに投げられたこのコマが、首をかしげたその姿勢のまま回り続けたら、へたなコマ回しは、じつは高名な手品師であった、ということになる。このようなパターンで着地したコマは、すぐさま首振り運動に入り、一気に回転半径を縮めて大地に直立する。最近のこどもたちはコマ遊びなどしないかもしれないが、これは一昔前のこどもにとっては常識である。

交流磁界を加えられたとたん、磁壁中に並ぶ磁気モーメントは首振り運動を起こす。その過程を、磁壁全体を通して眺めてみたのが、このモデルである。磁気モーメントの回転を表現するために、これまで立方体で描いてきた単位胞を球体として描いてみた。左の3つの球体が磁壁中の単位胞で、一番右側の１つが磁区の最端部に位置する単位胞という設定である。そして、HA方位に微弱な交流磁界を印加し、磁壁が単位胞1列分だけ右方へ移動する様子を追ってみた。このモデルにおける最大のハイライトは、単位胞の磁気モーメントが、そもそも何故に、xy平面から頭を持ち上げ、回転運動を始めるのか、であるが、じつは、くるくると回転しながら斜めに着地したコマの首振り運動と、ご覧いただいている磁気モーメントの首振り運動とは、基本的に同じ理屈に支配されている。コマに働いた地球の引力の作用と、上の球体モデルにおける交流磁界の"引力"を等価と考えれば、一見複雑そうにy軸を巡る赤い矢印にも古典力学の規律がしっかり利いている様子が見えてくる。

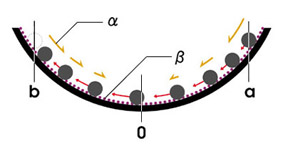
磁壁中の磁気モーメントは、磁区中の磁気モーメントと同様、(外から磁界が加えられなければ)xy平面上にピタリと身を寄せているが、その方位は、印加磁界Hの方位とずれている(このモデルでは３個の単位胞で磁壁を表現しているので、左から右へ45°、90°、135°と開いていく)。そこで、外部から磁界が印加されたとたんに、引力のある地球上に斜めに着地したコマと同じく、この角度の開きに起因して、トルクTが加わり、身を寄せていたxy平面に垂直に働くその力に背を押されるようにして、磁壁中の磁気モーメントは一斉に頭をもたげ、すぐさまy軸(印加磁界H方位)を中心とした回転運動に移ることになる。そのとき、矢印Lで示した制動因子が働かなければ、頭をもたげた磁壁中の磁気モーメントは減衰することなく固有の振動数でy軸の周りを回り続けることになるはずだが、磁壁は確かに移動するのだから、制動因子Lがしっかり働いていることは疑いなく、コマ同様、磁気モーメントも一気に頭を磁界方位に向けることになる(このモデルには、単位胞1列分の移動経過を示したが、印加磁界がさらに強まれば、y軸に頭を揃える、つまり左側の磁区に取り込まれる磁気モーメントが増加し、磁壁の欠員を補うように、右側の磁区に属する磁気モーメントが次々と磁壁に組み込まれていくことになる)。

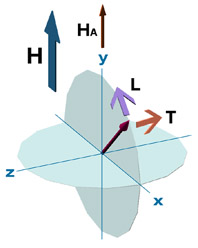
そこで、冒頭で触れたdM(磁気モーメントの変化)/dt(時間変化)であるが、これを、x、y、z軸の各成分に分解すると、dMx/dt,dMy/dt,dMz/dtとなる。しかし、上の球体モデルにおけるy軸は回転軸なので、この系におけるdMy/dtは常に0であり、時間的に変化しない。これは、磁壁中のすべての磁気モーメントについて言えることで、残るdMx,dMz成分の「変化量」も、すべての磁気モーメントにおいて同じ値となる。すなわち、xy平面に整然と並ぶ磁気モーメントがトルクTの力を受けて回転を始めてからdt時間後に、どの磁気モーメントも同じ平面内に存在することになり(面的な平行関係は崩れない)、たとえば下のモデル図に示すように、すべての磁気モーメントが同時に磁壁に直交する瞬間も頻発することになる(y軸を中心として回る磁気モーメントの方位が時間変化dtの間にx軸方位からどれくらいずれたかを示す量dφ/dt=角速度が同じなので、こういう結果となる)。つまり、磁壁の両側には、周期的に増減し、極性を転換する磁極が発生することになる。すると、そのエネルギーを低減するために、N極からS極へ向かう反磁界Hdが、磁極の強さに応じて磁壁内部に発生することになり、じつはこの力が、磁気モーメントをy軸に押しつける制動因子L(つまり、dMy/dt成分を増加させ、dMx/dt,dMz/dt成分を減少させる働き)として機能している。なお、反磁界Hdもマクロ的なレベルで出現すると、大変困った事態を招くが、その経緯については後節で詳しくお伝えしたい。