With ferrite by TDK

GRAIN49 ギガヘルツ帯の共鳴現象

ギガヘルツ帯の共鳴現象
補足(分裂するμの概念について)

ギガヘルツ帯の共鳴現象

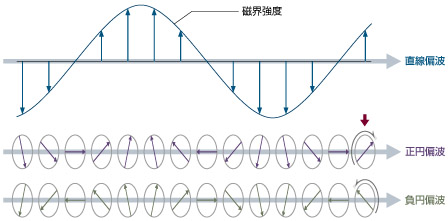
直流磁界を印加した円柱状のフェライト素子を通過するだけで、電磁波の偏波面はものの見事に回転する。そのミステリーを解く鍵は、直流磁界の方位に頭をきつく押さえつけられた磁気モーメントが、ついに大きく頭を振り始める現象に秘められているわけだが、その様子をなるべく具体的かつ正確にイメージするために、まずはその前段階、すなわち磁壁共鳴以降の磁気モーメントの挙動をμ値と関連させた磁気モーメントの回転モデルで確認しておきたい。

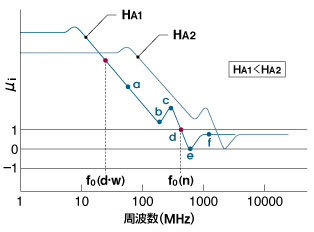
そこでまず、上に示したグラフのaポイント、すなわち磁壁共鳴f0(d・w)後の磁気モーメントの動きを、下のモデルで確認していただこう。GRAIN 28で詳しく見てきたように、磁気モーメントの固有振動数ωにはまだ至らないこの周波数レベルにおいては、磁区内磁気モーメントは刻々と変化するHeff方位に追随して、わずかながらμをかせいでいる(モデルa)。また、巨視的にはフェライト中の磁壁はグレインごとに三次元的にランダムな方位に移動しているので、aポイントにおいてもわずかながら移動可能な磁壁も存在するわけだが、しかし、交流磁界の周波数がじわじわと高まるにつれ、がんばり屋の磁壁もひとつふたつと動けなくなり、ついにμ値はグラフのbポイントまで落ち込んでしまうことになる。

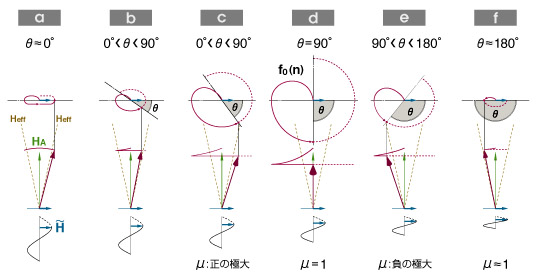
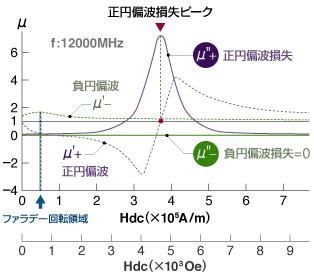
そして、モデルのbに示すとおり、そのときすでに、交流磁界の周期と磁気モーメントの回転周期の間には位相差θが生じており、周波数が高まるにつれ、その開きは徐々に大きくなるが、回転半径も大きく広がるので、グラフのcポイントにμの極大値が出現する(モデルc)。そして、その直後の自然共鳴周波数f0(n)で磁気モーメントの回転半径は最大となるが、このとき、位相差は、ちょうど90°となるため(モデルd)、磁気モーメントは磁化Iに寄与することができず、μは一気に1と化す(グラフのdポイント)。そして、さらに周波数を高めると、位相差は90°の一線を超えてしまうことになり、交流磁界の向きに対して磁気モーメントの向きが反対となる最悪の状況となる(モデルe)。その結果、μ値はグラフのeポイントに示す負の極大値に転がり落ちてしまい、さらに周波数が高まれば、180°の位相ずれをひきずりながら磁気モーメントの首振り半径はモデルfに示すとおり急速に収束し、μ値も1に限りなく迫ることになる(グラフのfポイント)。

さて、そこで、磁気モーメントの方位をことごとくHdc方位に揃えたくだんの素子に、自然共鳴周波数f0(n)を上回る高周波磁界を加えたモデルが下のgとhである。強力なHdcが加えられたので、Heffの向きも垂直に立つHA方位にかなり迫っている。磁気モーメントは強力な直流磁界に引きつけられているので蚊の鳴く程度にしか頭を振ることができず、μ値も下のグラフのgポイントに示すとおり、ほとんど1近傍を低迷することになる。

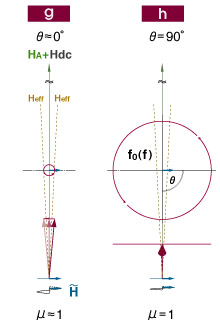
だが、Hdcの力によってギガヘルツ帯にシフトした磁気モーメントの固有振動数ωに交流磁界の周波数が迫るにつれ、自然共鳴に至るプロセス同様、磁気モーメントの回転周期と交流磁界の周期に"ずれ"が発生し、一気にその"ずれ"が開くとともに磁気モーメントの回転半径も急速に広がってμが極大に達した、かと思ったその直後に、位相差が90°に達する瞬間が訪れる(モデルh)。

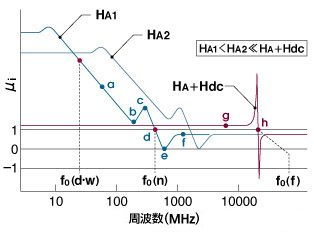
この共鳴現象(グラフのhポイント)は、直流磁界Hdcにより強制的に高められた磁気モーメントの固有振動数ωに対応するものなので、自然共鳴と区別して"強磁性共鳴"と呼ぶが、その発生機構は本質的に自然共鳴のそれと同じである。

また、上に並べた共鳴現象のモデル(dとh)は、磁気モーメントの回転周期と交流磁界の極性反転周期の間に生じる位相差がちょうど90°に達する瞬間に、磁気モーメントの固有振動数ωと交流磁界の周波数fが一致するかのようにも見えるが、それは、別々の現象が偶然の一致をみたということではなく、同じ現象を2つの角度から表現したものである。つまり、およそ共鳴と呼ばれる現象は、固有振動数ωと周波数fの一致と1/4の位相差が同時に起きることを意味しており、それ以外に共鳴現象が起きる状況はあり得ない。その様子を"体感"していただくには、下に描いた振り子の強制振動モデル、すなわちブランコ遊びの力の入れ具合を思い出していただくのがてっとり早い。振り子が最も大きく振れるのは、振り子の位置と力の入れ具合がちょうど1/4周期だけずれたときで、試しにこの"ずれ"がゼロの場合、あるいは1/2周期の場合など、いろいろなケースを思い描いていただくと、子供の時分に体得したあの感覚が、まさしく1/4の"周期ずれ"であったことに合点がいかれることと思う(なお、グラフに記したf0(f)の(f)は、「ferromagnetic resonance」の意)。

補足(分裂するμの概念について)

以前にご覧いただいたとおり、磁壁が身動きできなくなった後も、自然共鳴周波数f0(n)以前ならば、磁気モーメントのフットワークはなかなかに軽妙であり、右へ左へ目まぐるしく方位を転換する交流磁界の周期に遅れることなくピタリと追随したわけである。下はそのあたりの様子を見たGRAIN 25のモデルであるが、Heff方位の変化と、それに追随する磁気モーメントの動きは、まるで時計の振り子のようになめらかで乱れることもなく、交流磁界の方位と平行する二次平面上にへばりついている。

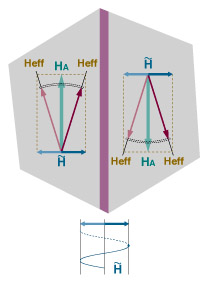
したがって、このような段階では磁化Iの意味も明快であり、単位体積中に含まれる磁気モーメントが磁界方位軸に投影する成分のベクトル和と考えておけばよかった。ところが、自然共鳴周波数を超えた高周波領域においては、交流磁界の方位と磁気モーメントのそれとの間に生じる"ずれ"のために、磁化Iの意味も、三次元的なものとしてとらえなおさなくてはならなくなる。

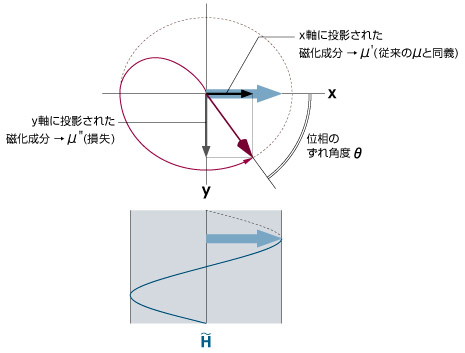
つまり、自然共鳴直前の状態を示す上のモデルのように、磁性の根源である磁気モーメント固有のボーア磁子量(単位胞単位)は、磁界の変化方位(x軸方位)ばかりでなく、位相のずれ角度θが開くにつれ、それと直交するy軸方位にも大きく影を落とすようになり、磁化Iもx軸成分とy軸成分に分割されることになる。

磁化Iが直交する2つの成分に分割されれば、μもそれぞれの成分に分割されなければおかしなことになる。そこで、このような位相ズレの生じた磁化機構におけるμを把握するために、単位磁界Hにおいて交流磁界方位(x軸)にいかほどの磁化Iが投影されるかをμ'で示し(これまで用いてきたμと同義である)、そのとき交流磁界方位と直交する方位(y軸)に投影される磁化Iに対応するμについては、μ"で表すことになった。断るまでもなく、μ"の増加はμ'の低下を意味する。つまり、位相ずれの増加にともなうμ"の増加は、そのまま磁化に伴う損失の増加を意味するわけで、それが位相差90°で最大となる理由については、ことさらな説明は不要であろう。

なお、自然共鳴や強磁性共鳴においては、交流磁界方位(x軸)に投影される磁化Iは0となるので、フェライト固有のμ'値、すなわちI(磁化)/H(磁界)も0となるはずである。物理的な現象としてはまさしくそのとおりなのだが、しかし、グラフの表記では、そのときのμ値は0ではなく「1」になっている。これはどうしたことか？　と思われるのは当然である。じつは、0が「1」となるこの不可思議には"実用上のちょっとした事情"がからんでいる。だが、いましばらくは、フェライト宇宙の中で起きている物理現象を"生"のまま観察していきたいので、0を1とするこの操作の内訳は、ギガヘルツ世界のしめくくりとなるGRAIN 58でご説明することにする。

TDKは磁性技術で世界をリードする総合電子部品メーカーです

TDKについて