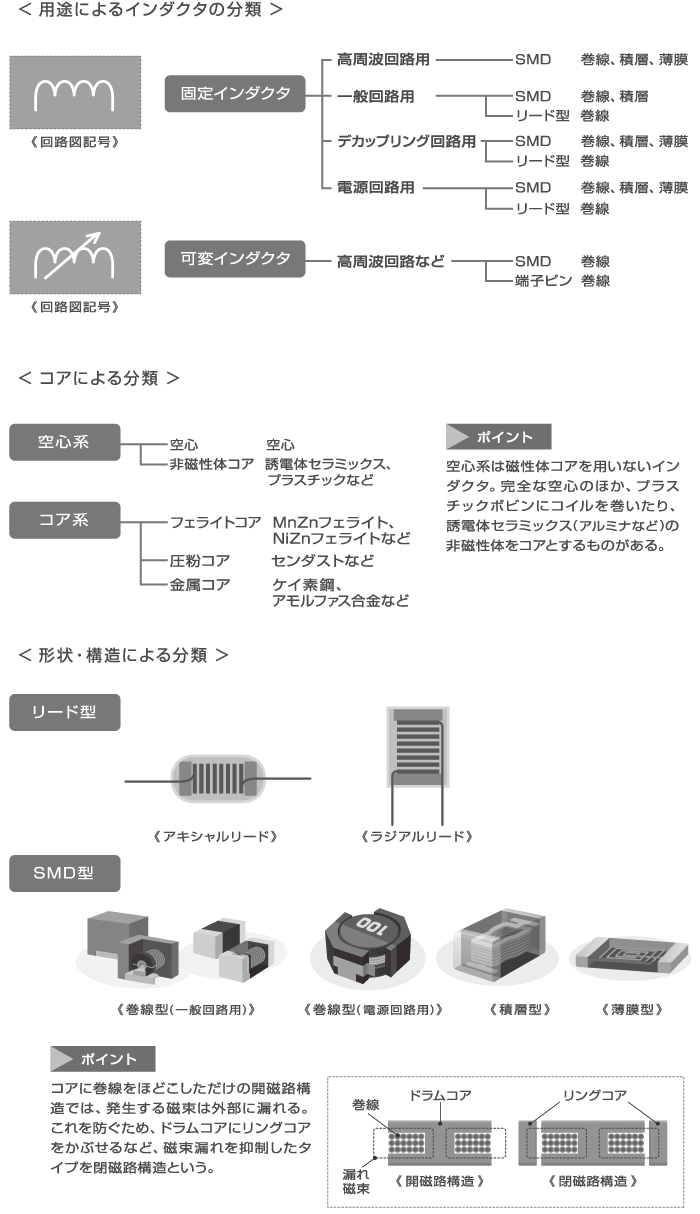
エレクトロニクス入門

インダクタ編 No.1「インダクタ（コイル）の基礎知識①」

インダクタ(コイル)は、抵抗、コンデンサとともに3大受動部品と呼ばれる電子部品です。電流に対してコイルが示す特性を利用して、電源回路や一般信号回路、高周波回路などで重要なはたらきを担っています。

電流の磁気作用とコイル
電磁誘導とコイルのインダクタンス
コイルの設計とインダクタンス

電流の磁気作用とコイル

電流は磁界をつくり、周囲に磁気作用を及ぼします。1820年、エルステッドによって発見された「電流の磁気作用」です。これにより、電流が同方向に流れる平行導線は互いに吸引しあい、電流が逆方向に流れる平行導線は互いに反発しあいます。この力の大きさを測定するため、アンペールは導線を枠状(角型)にして吊るした装置を製作しました。さらに、アンペールは導線を円筒状に巻いたコイルをつくり、これをソレノイドと呼びました。これがアンテナコイルなどに用いられるソレノイドコイルのルーツです。電流の流れるソレノイドコイルは磁石と同じ性質を示すことも、このころ発見されました。

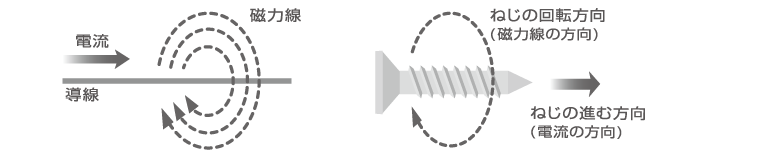
＜電流がつくる磁界と右ねじの法則＞

磁力線の方向は「右ねじの法則」で決まります。すなわち、右ねじの進む方向と回転方向は、それぞれ電流方向と磁力線の方向となります。

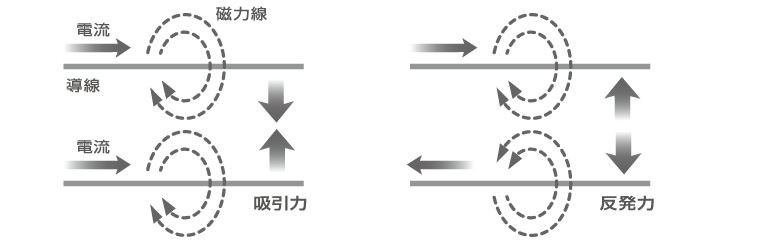
＜平行導線に加わる力＞

平行導線に流れる電流が同方向の場合、導線の間には吸引力が作用し、逆方向の場合は反発力が作用します。

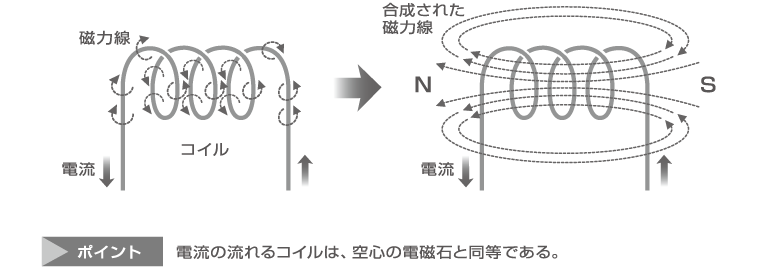
＜コイルと磁力線＞

コイルに電流を流すと、磁力線は合成されて、コイル内部を貫通するようになります。

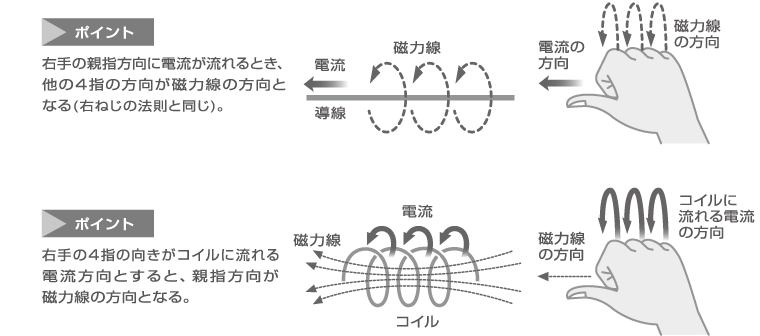
＜右手親指の法則＞

右手を利用して、電流や磁力線の方向を簡単に知る方法。

電磁誘導とコイルのインダクタンス

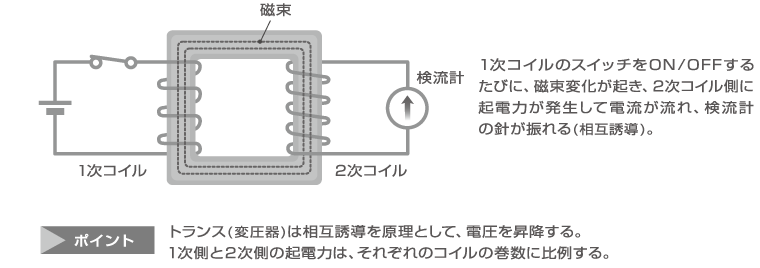
電流が磁力線を生む電流の磁気作用とは逆に、磁束変化が起電力を発生するという「電磁誘導(electromagnetic induction)」現象が、1831年、ファラデーによって発見されました。たとえば、環状の鉄心に2つのコイルを巻き、1次側のコイルに電池をつないでスイッチをON/OFFすると、2次側のコイルに起電力(誘導起電力)が発生して電流(誘導電流)が流れます。この電磁誘導現象を相互誘導といいます。

＜相互誘導＞

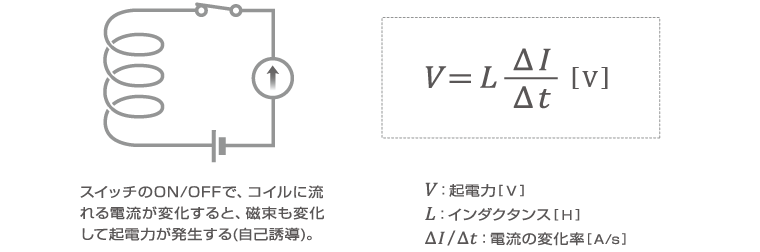
＜自己誘導とコイルのインダクタンス＞

単独のコイルでも電磁誘導現象が起こります。コイルに流れる電流が変化すると、発生する磁束も変化して、コイルに起電力が発生するのです。これを自己誘導といいます。その起電力(V)は以下の式で表され、比例定数Lを自己インダクタンスといいます。通常、インダクタ(コイル)のインダクタンスとは、この自己インダクタンスのことです。

インダクタンスはコイルにおける最も重要なパラメータで、コイルが発生する磁束(Φ)は、インダクタンス(L)と流れる電流(I)に比例します。

＜レンツの法則＞

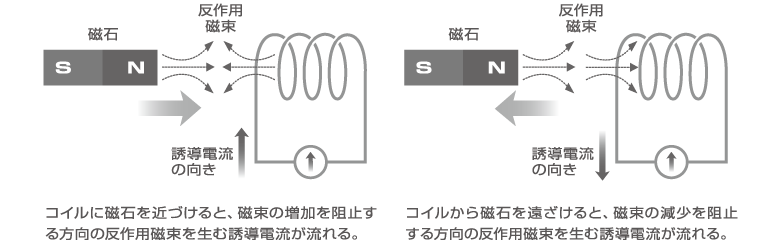
電磁誘導よって発生する誘導電流の向きを簡単に知る方法として、「レンツの法則」があります。誘導電流は、磁束変化あるいは電流変化を阻止して、元の状態を維持する方向に流れるという法則です。いわば「押さば押せ、引かば引け」の関係で、力学の反作用にも似ているので、反作用の法則とも呼ばれます。

コイルの設計とインダクタンス

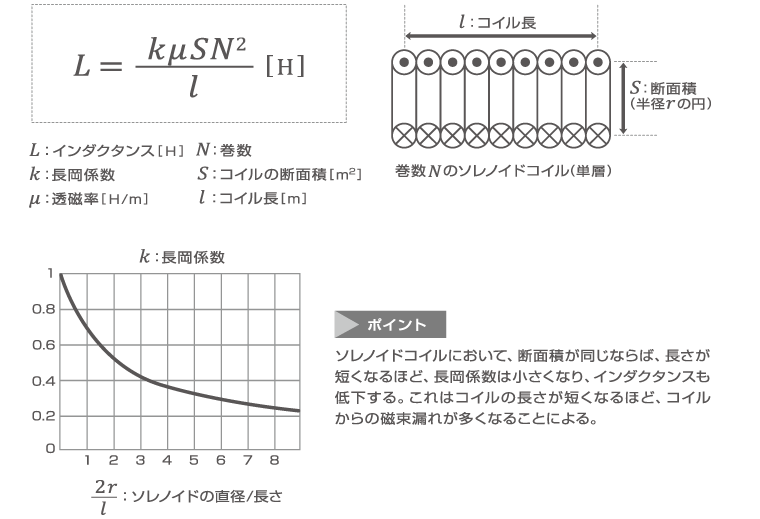
コイルのインダクタンスはコイルの形状によって変わってきます。たとえば、ソレノイドコイル(単層)のインダクタンスは、以下の式で求められます。長岡係数(k)は、物理学者・長岡半太郎博士によって導入されたもので、コイルの形状に対する補正係数です。断面積の半径r ・長さl のコイルにおいて、長岡係数は下のようなグラフとなります。2r/l ＝0は無限に長いコイルで、その長岡係数は1となり、有限長のコイルは1未満となります。これは断面積が同じならば、長さが短くなるほど、インダクタンスが低下することを意味します。

＜ソレノイドコイルのインダクタンス＞

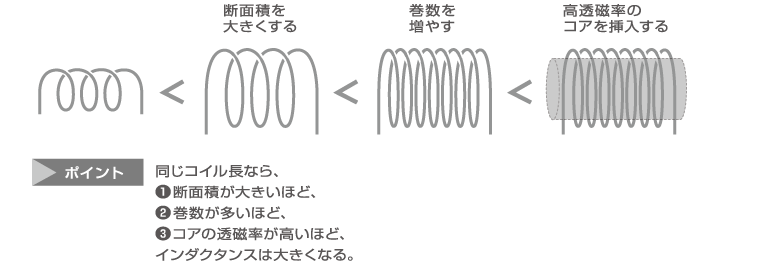
＜インダクタンスを大きくする基本手法＞

上記の式より、コイルのインダクタンスは、同じコイル長なら、断面積が大きいほど、巻数が多いほど、大きくなることがわかります。また、同じインダクタンス値なら、透磁率の高い磁性体をコア(磁心)とすることで、空心のコイルより格段にインダクタンスを大きくすることができます。透磁率とは磁束の集めやすさを表す指標で、磁化されやすい(磁化率の高い)物質ほど、透磁率は高くなります。

＜さまざまな物質の比透磁率＞

物質の透磁率を真空の透磁率との比で表したものを比透磁率(無単位)といいます。真空の比透磁率は1で、空気、水、銅、アルミニウムなどの弱磁性体(非磁性体)の比透磁率も、1前後にとどまります。これに対して、ニッケルや鉄、フェライト、電磁鋼など、軟磁性の強磁性体の比透磁率は、数100～10万以上にも及びます。軟磁性とは外部磁界によって磁化されやすく、外部磁界を除去すれば磁化を残さず、元の状態に戻る磁性体の性質です。

TDKは磁性技術で世界をリードする
総合電子部品メーカーです

TDKについて

エレクトロニクス入門

インダクタ編 No.1「インダクタ（コイル）の基礎知識①」